灵魂守卫

Inheritance Mode in C++

There are 3 kinds of inheritance mode: public private protected

we can change to each other between protected and public,but we can’t change private in base class to public or protected

 

在本文，我将比较透彻地讲解红黑树。本文适合那些有对二叉树有一定的基础，并且熟悉C语言的读者。本文最主要的参考资料是《Introduction to Algorithms 3rd Edition》。

1.1 二叉查找树

1.1.1 基本概念

二叉查找树是在数据结构中比较重要的数据结构之一，从外部看它满足集合性质，具有查找，插入和删除的基本功能，同时还可以求最大值和最小值。由于二叉查找树独特的性质，它特别适合用来存储动态集合。
定义：对于二叉树上的所有结点x，如果y是x的左子树，那么y.key ≤ x.key。如果y是x的右子树，那么y.key ≥ x.key，这样的二叉树就称为二叉查找树(Binary Search Tree)。
我们关心的二叉查找树的逻辑结构，下面的两棵二叉树：

图1 二叉查找树。(a)这一棵高度为3的二叉树，因为10比15小，所以10在15的左子树上；同理在以10为根的左子树里，7比10小所以7在左子树上，12在10为根的子树的右子树上；20在以15为根的右子树上。(b)这是一棵高度是4的二叉查找树，它的所有key与图(a)是一样的。在图(a)中，查找最坏的情况是7和12，它们需要经过3次比较才能找到，而图(b)最坏情况是20，需要经过4次比较才能找到。
要想二叉树的查找的花费时间小，我们尽可能让二叉树不出现类以于单链形态的二叉树，让树的高度尽量的低。对于高度为h的二叉查找树，从树根对叶子最坏的情况是比较h次。也就是说，对于高度为h的二叉查找树的最坏查找情况的运行时间是O(h)。二叉树的查找效率取决于树的高度。

1.1.2 操作

二叉树做为动态集，它有查找、插入、删除、最大值、最小值、前驱和后继这些基本操作。为了后序的方便，我们定义了结点和树，另外我们还用NIL表示空子树。

查找
在二叉查找树中根据给定的key找到该结点。由于二叉树的性质，我们就知道，如果目标key比当前结点的key要小，那么目标结点必定在当前结点的左子树上。

最小值与最大值
我们来分析一下最小值的位置。我们认为最小值的位置是从根出发一直沿结点的左子树直到某个结点x的左子树为空，那么这个结点x就是整个二叉树中key最小的结点。注意，我们并没有做任何key的比较。
证明：假设这个结点x不是最小值，另外有最小值结点y，那么y.k > x.k。如果y是x的祖先，因为x位于y的左子树上，那么x肯于定比y要小，所以y不是x的祖先。如果y不是x的祖先，假设y与x的最小的共同祖先的z，又因为y不是x的祖先，所以y在z的右子树上，所以z.k < y.k，并且有z.k > x.k，与假设的y.k > x.k矛盾，所以假设不成立，x是二叉查找树中key最小结点。最大值的分析方法也是一样的。

前驱和后继
前驱与后继定义来源于二叉树中序遍历的key序列。我们知道二叉的中序遍历的key序列是一个升序序列。在二叉查找树中，对于结点x，如果有结点y，满足y.key>x.key并且y是这些结点中key最小的，那么y就称之为x的后继。同理，在二叉查找树中，对于结点x，如果有结点y，满足y.key

图2结点的后继和前驱。(a)y是x的后继，因为y没有左子树，所以y是x右子树上key最小的结点。(b)y是x的后继，因为x的左子不为空，所以y是x左子树中最左那个小那个，所以y是x的后继。(c)x是y的前驱，因为y没有左子树，所以y是x左子树上key最大的那个结点。(d)y是x的前驱，因为x有左子树，所以x左子树上key最大的在x左子树上最右的那个结点。也有可能是z右孩子的最左的那个子孙结点(图b所示)。如果y是的后继，那么y就是x的前驱。
对于某个结点y它的后继的位置是：如果y的右子树存在，那么后继是y的右子树中的key最小的结点；如果y的右子树不存在，那么我们只要找到哪个结点的前驱是y，那么那个结点就是y的后继(图2中的d)。

根据前驱和后继的定义，我们知道通过对树中最小值一直沿着后继直到结束，这样的序列就是中序遍历的序列。下面给出中序遍历的代码：

插入
对二叉查找树的插入，不能破坏二叉查找树的性质，那么我们要结点插入到什么地方呢？答案是叶子，新插入的结点，都是将成为某个叶子结点的左孩子或者右孩子。

图3 二叉查找树的插入。图中key为11的结点插入到树中，其中浅色结点表示插入时候比较的路径。虚线表示插入的位置。

我们发现insert与search方法是一样的，只不过search是查找特定的key，而insert是查找合适的叶子结点的位置，它的运行时间为O(n)。

删除
在介绍删除二叉查找算法之前，我们先来介绍一个辅助函数transplant，这个函数有3个参数，在树T中，将v替换u的位置，即u的双亲变成v的双亲，v替换u成为u双亲的孩子。另外一个辅助函数replace，这个函数有3个参数，在树T中，将v完全代替u，即u的双亲变成v的双亲，v替换u成为u双亲的孩子，另外左右孩子均为u的孩子。

图4演示了transplant中v在树中替换u的过程。如果u是根，即v.p==0时，T的树根就改变了。

我们来考查一下待删除的结点是z。那么z可能有几种情况：

• z没有右孩子；
• z有右孩子：z的右孩子有左孩子，z的右孩子没有左孩子。

图5 二叉树删除的三种情形。图中z（浅色的）为待删除的结点。(a)没有右孩子的删除，将z的左孩子替换z即可，z的左孩子有可能是NIL指针。(b)z的右孩子不为空,y是z的后继，但右孩子的左孩子为空，我们知道z的右孩子就是z的继，所以用z的右孩子替换z即可。(c)z的后继y不是z的右孩子，y的右孩子替换y，从树中移出y，将y作为z右孩子的双亲连接上，此时情形成了情形b了。
下面我具体针对这3种情形进行分解。情形1，z没有右孩子，我们只要将左孩子替换z在树中位置就能完成删除操作，其实我们拿z的前驱替换也是可以的；情形2，z有右孩子，所以我们找到z的后继替换z。因为z的key小于右子树所有的key（假设没有重复的key），那么z的后继就是右子树上的最小key。如图5的中b和c，z的后继可能是z的右孩子（当右孩子没有左孩子就会出现该情况），那么调用transplant(T,z,y)。另外，要连接上原来z的左子树；z的后继也有可能不是z的右孩子（图c所示的情况），首先我们调用transplant(T,y,y->r)，这时候y已经从树中脱离了，然后我们将y嫁接到z的右孩子的双亲上，这样y就成了z右孩子的双亲了，这和情形b是同一种情况了。下面是删除的代码：

1.1.3 实现

参考附件：bstree.c。

1.1.4 思考题

1.Bunyan教授认为他发现了二叉查找树的一个重要的性质。假设在二叉查找树上查找key为k的结点,并且key为k的结点是一个叶子结点。那么有三个集合：A，搜索路径的左边结点的集合；B，搜索路径上的结点的集合；C是搜索路径右边的结点集合。Buyan教授认为对于三个集合的任意值a∈A，b∈B，c∈C一定满足a≤b≤c。对于上面的观点，请给出最小可能一个的反例。
2.证明：在高度为h的二叉查找树上，我们实现的动态集基本操作:min，max，successor，predecessor，search，insert和remove的运行时间都是O(h)。
3.在二叉查找树的删除操作中，假设我们不取z的后继而取z的前驱替换z，请相应对称的代码。

1.2 红黑树

在上节的思考题中，我们证明了在高度为h的二叉查找树上，我们实现的动态集基本操作运行时间都是O(h)。总而言之，树度h决定查找效率。如果我们通过某种方法能够将二叉树尽可能的低，那么二叉树的查找效率将会大大地提高。
对于一个含有n结点的最坏的情况是这n个结点形成一条单链，那么二叉查找树的树高为n，运行时间为O(n)；那么最好情况是n个结点形了一棵完全二叉树。所谓完全二叉树是指对于一棵高度为h的二叉树，除第h层外，其它各层的结点数都达到最大个数，并且第h层所有的结点都连续集中在最左边，这样的二叉树称为完全二叉树。那么h介于lg n与lg n+1之间，也就是说运行时间为O(lg n)。可以说它的效率是极高的。

1.2.1 基本概念

如果我把二叉查找树的每个结点都涂上红色或者黑色。如果它满足下面的5个性质，那么我们就称它为红黑树（Red Black Tree）：

• 每个结点不是红色就是黑色。
• 根结点是黑色的。
• 每个叶子结点（NIL）都是黑色的。
• 如果一个结点是红色的，那么它所有的孩子都是黑色的。
• 对于每一个结点，从当前结点到后代的叶子的路径上包含黑色结点的数量是相同的。

根据红黑树的性质，我们可得出下面的结论：具有n内部结点的红黑树的高度最高为2lg(n+1)。
在证明这个结论之前，我们来看看红黑树的表示。每个结点到叶子结点（NIL）经过的黑色结点的个数（包括自已）称之为黑高度(black-height)。我们把NIL称之为外部结点，那些带有key的“合法”的结点称之为内部结点。

图6 红黑树的表示。key为64的结点的黑高度为3，key为26，81，14，44的结点黑高度为2，key为5，19，30，76，92的结点黑高度为1。
证明：我们将红色结点吸附到黑色的双亲结点上，那么一个黑色结点最多可以吸附2个结点，并且可以有4个孩子，那么就形成了一个大结点，如图7所示。这样树我称之为234树。红黑树的数学本质就是234树，并且所有的“叶子”结点的高度都是相等的。不难看出，黑高度就是这棵234树的高度。

图7 将图6中的红色结点吸附到双亲结点上，这样对应数学结构为234树。
对于高度为h并且所有的“叶子”结点的高度都是相等的234树最少有多少个结点呢？要想结点最少，那么它就退化出了满二叉树了。所以，树的结点个数n满足：
（公式1）
由公式1得出：两边取对数即。这里的h是234树的高度，由前面所述，红黑数的黑高度就是对应234树的高度。对于黑高度了h，由性质2、3、4得出红色结点不可能多于黑色结点。所以结点个数不大于黑高度的2倍。所以具有n内部结点的红黑树的高度最高为2lg(n+1)，证毕。
我们证明的结论说明红黑树的搜索运行时间为O(2lg(n+1))也就是O(lg n)。
为了方便操作，我们引入一个NIL结点，这个NIL结点是跟普通的结点一样，不过我们只使用color这个域，因为NIL结点是黑色的。

我们定义了结点的颜色，同时每个结点都增加了一个c域来表示结点的颜色。除此之外我们还为树定义了一个nil结点，之前实现的二叉查找树中指向NIL都改为指向T->nil。

1.2.2 查找

因为红黑树本身就是一棵二叉查找树，所以对红黑树的查找操作跟普通的二叉查找树的操作没有什么不一样，但注意的时，在这里我们已经用T.nil取代了0。下面仅仅给出查找操作的代码，读者可以比较一下与普通的二叉查找树有什么不一样的地方。

有两处不一样，第一处是x!=0替换成了x!=&T->nil，另外一处是在结尾出增加了对x是否是nil的判断，操作上的代码没有二致。对于前驱和后继，我就不举例了，有兴趣的读者可以自行思考或者参考一下附件的实现。

1.2.3 旋转

在介绍红黑色的插入与删除前，我们介绍一下二叉树的旋转操作：旋转分为左旋(Left-Rotate)和右旋(Right-Rotate)。
左旋

图8 树的左旋和右旋。(a)将x结点右孩子y替换x成树中的位置，同时x成为y的左孩子，y原来的左孩子成为x的右孩子。观察在调整前α　　下面是左旋代码，先用y替换x的位置，再将y的原左子树变成x的右子树，x成y的左子树。

右旋
下面给出右旋的代码，先用y替换x的位置，再将y的原右子树变成x的左子树，x成y的右子树。

小技巧：区分左旋还是右旋，我们只要看x最终是y的左孩子还是右孩子，如果左孩子那就是左旋，如果右孩子那就是右旋。
综述，二叉查找树的左旋和右旋并不会破坏其二叉查找树的数学性质。

1.2.4 插入

红黑树的插入前半部分与普通的二叉查找树的插入大致相同的，我们来看一下插入的代码。

从代码中可以看出，它与我们前面的二叉查找树的插入操作有两个地方不同，首先是用T.nil取代了0，其次是在代码的结尾，多出了两行，一行是z->c=RBT_RED,另一行是调用了_rbt_insert_fixup函数。
我们知道，将结点插入到红色黑树的叶子结点上，可能会导致这棵树不再满足红黑树的性质。我们将新插入的结点着成红色，插入到红黑中，然后通过_rbt_insert_fixup修正红黑树的性质。
当插入结点z时，我如果把z着成红色，看看我们会破坏原有的那些性质呢？
我们已经将z着成红色了，所以性质1不会被破坏。当往空的红黑树插入结点的时候，这个性质2会被破坏。每个叶子结点（NIL）都是黑色的，所以性质3不会被破坏。因为我们插入的结点是红色的，所以性质4可能被破坏，同样是因为我们插入的是红色结点，所以性质5不会被破坏。综述，我们往将z着成红色插入到红黑树的时候，可能会破坏性质2和性质4，其它性质不会被破坏。

图9 红黑树的插入情形。(a)z的叔叔是红色的，z是左孩子;(b)z的叔叔是红色的，z是右孩子;(c)z的叔叔是黑色的，z是左孩子;(d)z的叔叔是黑色的，z是右孩子。这里我们略了z的叔叔是左孩子的情况，因为它们是对称的。
当结点z插入时，如果z的双亲结点不是红色的，那么它不会破坏红黑树的性质。所以只有z的双亲是红色的时候，z和z的双亲都是红色会破坏红黑树的性质4，所以我们目的是在不破坏现有的性质1,3,5来恢复性质2和4。
我们考查z和z的叔叔，当z的双亲是左孩子，性质4被破坏的情况只有图9所示的4种情况；当z的双亲是右孩子的时候，跟这个是对称的。我们知道，是因为性质4被破坏了，所以z和z的双亲都红色的，所以z双亲肯定不是根结点，因为根结点是黑色的。下面针对这四种情况进行恢复红黑色树的性质。
情形1：z的叔叔是红色的。
这种情况，不管z是右孩子还是左孩子，我们将z的双亲的双亲上的黑色的分别涂给z的双亲和z的叔叔，这样不会可能破坏性质2或者性质4，其它性质依然保持，因为z的双亲是红色且z的叔叔也是红色的(假设的条件)。我们不知道z的祖亲的双亲颜色，所以我把z的祖亲当作新的结点z，继续调整。

图10 我们将z.p和叔叔都着成黑色，z.p.p当作新的z继续修复。直到z.p的颜色是黑色的，那么z.p.p是根时，由于z.p是T.nil，它也是黑色的，也会退出循环，不会将叶子着成红色的。我们在最后恢复性质2，暂且不考虑性质2被破坏。
情形2：z的叔叔是黑色的，z是双亲的左孩子。

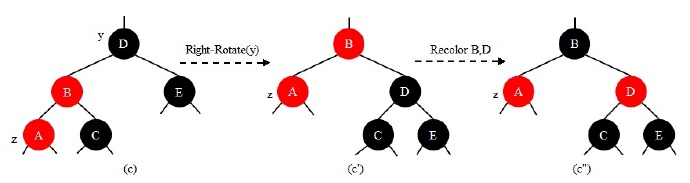
图11 情形2。我们发现可以将B右旋到右子树，通过一次右旋和着色就可以恢复红黑树的性质4了，因为没有哪个红结点是红色的孩子双亲。
进入每一个情形都是因为z和z.p都红色的，由于插入之前是合法的红黑树，所以z.p的另一个孩子是黑的，z.p.p也黑色的，图示的y是是z.p.p，所以y是黑色的。对y进行右旋，我们发现通过z的路径少了一个黑色，如图示交换一下颜色就恢复了红黑树的性质4了。
情形3：z的叔叔是黑色的，z是双亲的右孩子。

图12 情形3。z的叔叔是黑色的，并且z是右孩子。
我们发现对z的双亲y进行左旋，因为只有z和z的双亲不满足红色树的性质4，所以z的左右孩子都是黑色的，这样旋转并不会破坏z的孩子和z兄弟的黑高度的。然后把z指向z的左孩子，这时候就将情形3转换到了情形2了。
下面是修复红黑树四种情形的代码。最后，我们修复了根是黑色的性质2。

从上面的修复性质4的可以看，只有情形一在不做旋转的情况下，z的指针向上在树中移动两层。情形2经过一次旋转就可以恢复，情形3要先通过旋转变成情形2。所以我们得出结论，向红黑树中新插入一个结点着成红色，我们可以通过不超过两次的旋转就可以恢复红黑树的性质。

1.2.5 删除

红黑树的删除，其实也是先进行二叉查找树的删除，再调整颜色。
二叉树删除的三种情况中，对比观察图13，情况c中，使用y替换了z,只要我们将y着成z的颜色，那么我们很容易发现一个共同之处，那就是如果我们将虚线圈起来当成一个特殊的结点，那么所有从根结点出发经过双亲结点到达NIL树叶结点的路径肯定也经过孩子结点。那么二叉树删除的结果就是，圈中少了一个结点，如果我们将结点删除，但颜色保留，将刚移走的结点的颜色“塞”给x，也就是圈中的剩下的结点x,加上自身的颜色，此时x可能是“黑黑”也有可能是“红黑”。那么我们发现剩下的部分，除了性质1外，其它性质都没有变化。

图13 红黑树结点删除的初始情形。内圏的颜色是表示孩子的颜色，圈外表示双亲的颜色。x表示原删除或移走后剩下的结点的位置。(a)x的位置是z的左孩子，留下了z的颜色；(b)x的位置是z的右孩子，z的右孩子替换了z，留下了z右孩子的颜色；(c)x的位置是z后继的位置，z的后继已经替换了z，留下了原z后继的颜色。
我们发现一个规律，如果圈内有一红一黑，那么我们并不需要调整红黑树，直接将x着成黑色就行了。所以我们删除代码比之前普通二叉查找树的删除多了一些记录位置的代码 。还有一个值得注意的地方就是如果圈中的孩子是叶子结点，那么通过叶子结点是无法找到双亲的，所以我们不管是不是叶子结点都将p指向圈中双亲的双亲。

好了，现在我们可以开始调整“塞”给x上的黑色了，根据判断条件，只要x和y有一个是红色，均不用调整，而且调整前是合法的红黑树，x和y不可能同为红色，所以唯一的情况是x是黑色，被移走结点留下的也是黑色。下图所示的x的兄弟w都是右子树的例子，同样如果w是左子树是对称的。

图14 上面是分别是调整颜色是遇到的所有情况。(a)情形1，w颜色为黑色的，并且w的右孩子为红色，这时候，我们对x的双亲左旋转将x的新双亲和新叔叔都着成黑色，x的祖亲着成原x的双亲的颜色。(b)情形2,w颜色是黑色的，并且w的左孩子是红色的w的右孩子是黑色的，将w进行一次右转，重新着色，我们发现这个状态正好是情形1。(c)情形3,w的是黑色的并且左右孩子都是黑色的，我们将x和w都提取一个黑色给x的双亲，这时候我们把双亲看成新的x，继续调整。(d)情形4，w颜色是红色的，由于w是颜色是红色的，所以w的左右孩子都是黑色的。我们对x的双亲做一次左旋，重新着色，我们发现状态转换到了(a)(b)(c)中的任意一种了。
假设有函数C(m)表示如果m结点是黑色的，C(m) = 1；如果m结点是红色的C(m) = 0。并且我们知道x是双黑的，所以w不可能是nil结点，所以w是有左右孩子的。
情形1:x的兄弟w是黑色的，并且w的右孩子是红色的。
我们假设C(x.p)=p，C(x.r)=q。在调整前：
α子树的根到图示的根黑结点个数是2+p；
β、γ子树的根到图示的根黑结点的个数是2+p+q；
δ、ε、ζ子树的根到图示的根黑结点的个数是1+q’’。
我们交换w和x双亲的颜色，并将w的右孩子着成黑色，再对x.p执行一次左旋。我们发现在调整后：
α子树的根到图示的根黑结点个数是3+p；
β、γ子树的根到图示的根黑结点的个数是3+p+q；
δ、ε、ζ子树的根到图示的根黑结点的个数是1+q’’。
α、β和γ均比之前多了一个黑色，如果我们将x身上的额外的黑色去掉，那么α、β和γ到图示的黑结点个数与调整之前一样，分别是2+p和2+p+q，调整结束。

情形2:x的兄弟w是黑色的，并且w的左孩子是红色的。右孩子是黑色的。
这个情形比较简单，我们交换一下w和右孩子的颜色执行一次右旋，α、β、γ、δ、ε和ζ到图示的根的黑结点个数仍然不变，观察这个情形就转化了情形1了。

情形3:x的兄弟w是黑色的，并且w的左孩子是黑色的，右孩子也是黑色的。
因为w和左右孩子都是黑色的，并且x是“双黑的”，将w和x的黑色都向上提，这时候将w着成红色。x的双亲成了新的x了，继续向上调整。

情形4:x的兄弟w是红色的。
因为x是红色的，所以x的孩子和x的双亲都是黑色的，调换w的双亲与w的颜色进行一次左旋。我们发现x的新兄弟成了黑色，那么这就成情形1、2和3中的任意一种来调整了。
下面是fixup代码：

1.2.6 实现

参考附件：rbtree.c。

1.2.7 思考题

1. 先依次画出从初始空树中成功插入key为41，38，31，12，19，8的结点的红黑树。再画出依次删除8，12，19，31，38，41之成功后红黑树。

附件

bstree.c : 二叉查找树实现代码
rbtree.h : 红黑树的接口
rbtree.c : 红黑树的实现
如果你是windows用户
main.c :红黑树的操作实例
rbtree.exe：一个红黑树的操作实例编译方法: gcc -o rbree.exe rbtree.c main.c -mwindows
本文的其它参考文档：
第12章 二叉查找树
第13章 红黑树
全文下载：红黑树详解